Definição de Matriz em Programação

Dentro de programação, matrizes são um agrupamento de variáveis do mesmo tipo, organizada em linhas e colunas. A forma de declaração da matriz em C é:

Assim, uma matriz de 3 linhas e 4 colunas int fizemos:

De forma gráfica:

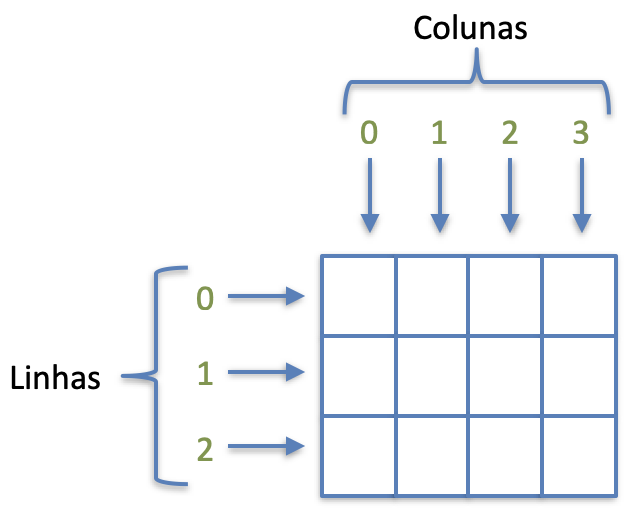
Assim como o vetor, a matriz tem as linhas e colunas começado em 0 (zero)

Formas de criar (declarar) uma matriz

De forma simples, temos as seguintes formas de declarar matrizes

1. Na forma 1, a matriz é declarada sem os valores, o C irá preencher as células com valores aleatórios da memória
2. Podemos declarar a matriz com todas as dimensões e valores, conforme a Forma 2. Nesse caso, verifique que o número de colunas é menor do que foi especifica, nesse caso, o C irá preencher as colunas com valores aleatórios.
3. Conforme podemos perceber forma 3, o número de linhas na declaração omitida, isso pode ser feito quando os valores forem declarados. Assim como na forma anterior, os valores podem ser omitidos, mas se forem inseridos mais valores do que foi declarado, um aviso de alerta será gerado

Acessando os elementos de uma matriz

A lógica de acesso segue semelhante a forma de acesso a um vetor, com os índices de linhas e colunas começando em 0:

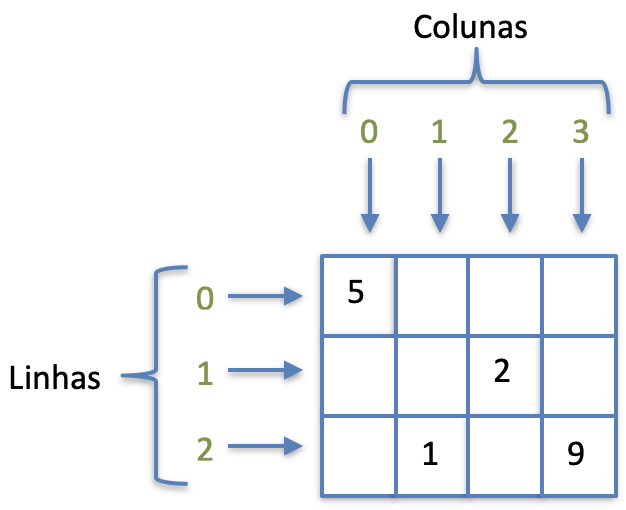
Para atribuir valores::

De forma gráfica, a matriz terá os seguintes valores:

Veja um exemplo de programa:

Matrizes e laço de repetição

Para percorrer uma matriz são necessários dois laços de repetição, um para percorrer as linhas e outros as colunas. Verifique a execução passo-a-passo do programa:

E o programa no ambiente do Replit:

Exemplo 1 - Lendo e armazenando as notas dos alunos

Faça um programa que leia 3 notas de 5 alunos e calcule a média das notas de cada alunos.

Como sabemos que são 5 alunos e cada aluno com 3 notas, iremos criar uma matriz de 5 linhas e 3 colunas

Adicionando um laço de repetição para percorrer os 5 alunos:

Para cada aluno, iremos fazer um laço de repetição para solicitar as 3 notas e armazenar na posição da matriz:

Agora iremos criar os laços de repetição para percorrer a matriz:

E para cada aluno iremos somar as notas, verifique que precisamos iniciar a variável int soma = 0; para cada aluno de forma que essa variável não some as notas dos alunos de outras linhas:

E ao final de cada execução das colunas, apresentamos a média:

No ambiente de desenvolvimento:

Exemplo 2 - Matriz diagonal superior

Dada a matriz a seguir, faça um programa que imprima apenas os elementos da diagonal superior:

Inicialmente vamos abordar o conceito de Matriz superior, em Álgebra Linear, matriz superior é uma matriz em que os elementos acima da diagonal principal não são nulos.

E a diagonal principal são os elementos em que a linha e a coluna possuem os mesmos índices, destacados abaixo na cor vermelha, abaixo, em verde, estão a posição da linha e coluna respectivamente:

Portanto, a diagonal superior são os elementos marcados em azul, com seus respectivos índices em verde:

A particularidade dos elementos de uma matriz matriz superior é que o valor da \(linha\) deve ser menor ou igual ao da \(coluna\), em programação, considerando que \(linha = i\) e \(coluna = j\) temos: i <= j

Que será a condição para exibição dentro do laço de repetição:

O programa em execução:

E passo-a-passo (aguarde que é lento para carregar mesmo!):

Atividades

• 1. Faça um programa que leia uma matriz de 3 x 3 elementos usando comandos de repetição, multiplique cada elemento por 5 e imprime o resultado.
• 2. Através de laços de repetição e decisão imprima uma matriz com 5 linhas e 5 colunas tal que o valor de cada elemento depende das condições abaixo (onde \(i\) é o índice da linha e \(j\) o índice da coluna): \[\begin{cases} 2 \textrm{ se } i>j \\ 1 \textrm{ se } i = j \\ -2 \textrm{ se } i < j \end{cases} \]
• 3. Faça um programa que receba duas matrizes de dimensões 3x3 e apresente a soma de seus elementos